Part 1: Planar Planforms

Abstract

It is widely believed that an elliptical span loading produces the minimum induced drag for a lifting surface. In general, the optimal span loading is quite different and the elliptical loading is only optimal for the restricted case of an isolated planar wing in uniform flow. The correct conditions of optimality, as derived by Munk for minimum induced drag for a given span and by Jones for minimum induced drag with a moment constraint, are applied by means of an inverse lifting line technique. Validation of the method by comparison with test data and classic theoretical results is shown.

Design charts showing optimal span loadings, planform shapes, induced drags, and centers of effort are derived for isolated surfaces, single sails in ground effect, twin sail biplane rigs, and hydrofoils operating at high speed near the water surface are presented. The application of the method to the design of optimal keel winglets is also shown.

Introduction

The efficiency of a sail rig is determined by its ability to generate a large amount of aerodynamic lift with a minimum amount of drag. Both the maximum lift and the drag are determined in part by viscous effects in the boundary layer and the surrounding inviscid flow - especially the wake.

Figure 1 presents a schematic view of the flow around a sail rig. The lift created by the sail results in deflecting the wind sideways, and this deflection takes the form of a trailing vortex sheet which wraps up into two large counter-rotating vortices. For rigs of moderate to high aspect ratio, the aerodynamics can be computed with reasonable accuracy by separating the three-dimensional flow problem into two separate two-dimensional flow problems: the flow about a section of the sail cut by a plane perpendicular to the axis of the sail, and the computation of the local flow conditions at the section which are determined by the wake. It is the second problem that is the subject of this paper.

The effect of the trailing vortex sheet shed into the wake is to induce a shift in the relative wind at the sail which reduces the local angle of attack and also rotates the lift vector (which is defined to be perpendicular to the local apparent wind) aft, which results in a component of the local lift which is in the free stream direction. This component is known as the induced drag. The velocities induced by the wake, and thus the local angles of attack for the sail, can be determined by looking at the configuration of the trailing vortices in a downstream plane perpendicular to the apparent wind called the Treftz plane.

Section design is primarily concerned with viscous effects. When measured relative to the section's zero lift line, most sections produce much the same amount of lift at the same angle of attack. So the art of section design consists of controlling the boundary layer through the pressure distribution so as to increase the maximum lift of the section and decrease the viscous drag. This leaves controlling the inviscid flow to the design of the planform.

The design of the planform, through its effect on the wake in the Treftz plane, seeks to maximize lift by ensuring that some portions of the sail do not operate above their maximum angle of attack while other portions operate well below their limit. Planform design also determines the lift-induced drag, which is the major drag component of a well designed rig at high angles of attack. Accomplishing these two goals simultaneously is one of the few happy coincidences in yacht design that doesn't require reaching a compromise between conflicting requirements, since minimizing the induced drag tends to lead to more uniform conditions over the sail, which aids in achieving maximum lift.

Several authors have used optimization techniques to determine the best sail plan. Greely et al (1989) used quadratic programming with a lifting line analysis to generate spanloads which maximized the net thrust, including the effects of viscous drag. When using Lagrange multipliers to do the optimization, they experienced difficulties with the technique trying to use negative lift at the head to meet the heeling moment constraint.

Day (1991) used simulated annealing with a lifting line analysis to determine lift distributions which maximized the performance of a sailboard. Both induced drag and a simple viscous drag estimate were used to model the sail. He found that due to a constraint on heeling moment, the optimum spanload distributions had a negative lift at the head. Day's optimum distributions were shown to be similar to those of Wood and Tan (1975). Day (1995) also used a genetic algorithm to optimize the parameters of a sloop rig having triangular sails, in conjunction with various hull models.

However, the author has not found any source which handles the optimization of sail planforms in a comprehensive and general way, or that provides insight into the difference between the contributions of the inviscid vs. viscous portions of the drag and lift. All of the papers cited used a hybrid approach, in which an analysis method was coupled with an optimization technique in order to vary the geometric parameters and arrive at the best performance.

An alternative approach is to use an inverse method, in which the desired aerodynamic characteristics are specified first, and then the shape required to satisfy them is computed. Inverse methods may not always yield a shape which can be practically constructed, but they are very useful for determining shapes that are unconventional, and for defining what performance is possible. Armed with this knowledge, the designer can assess the impact of a more practical configuration which is close to the optimal shape. Often the performance degradation is minimal.

Minimizing Induced Drag

Day (1995) states that "If the rig is of high aspect ratio and low sweep angle, then the application of this criterion [lift to drag ratio] will lead to the well known result of an elliptical distribution of lift in the spanwise direction." As will be shown in this paper, this statement is not correct for the case of sail plans with a gap between surface and foot, when heeling moment is constrained, and for vertical hydrofoils.

Munk's 1923 paper established a number of important theorems regarding lifting surfaces and their induced drag. One, known as Munk's stagger theorem, states that the total induced drag of a system of lifting surfaces is independent of the streamwise position of the surfaces, provided that their loading is unchanged. This makes it possible to project all the surfaces into one transverse plane for analysis.

Munk's criteria for minimizing the induced drag is less well known: "Let the dimensions of a system of aerofoils be given, those in the direction of flight being small in comparison with those in other directions. Let the lift be everywhere directed vertically. Under these conditions, the downwash produced by the longitudinal vortices must be uniform at all points on the aerofoils in order that there may be a minimum of drag for a given total lift." "If all lifting elements are in one transverse plane, the component of the velocity perpendicular to the wings, produced by the longitudinal vortices, must be proportional, at all lifting elements, to the cosine of the angle of lateral inclination." Having the induced velocity normal to the surface be constant and proportional to the cosine of the dihedral angle corresponds to the wake leaving the surface as though it were a solid sheet sliding linearly with no distortions.

Notice that he says nothing about the shape of the spanloading. Most aerodynamic texts use a Fourier series to represent the spanloading and solve for the minimum induced drag of an isolated planar wing in a uniform flow. The result is the classical elliptical loading and this is said to result in a constant downwash. In fact, Munk shows that the converse is true! The induced drag is a minimum because the downwash is constant, and the elliptical loading is, for this particular case, the loading required to generate the constant downwash.

Jones (1950) later showed that when the wingroot bending moment is constrained, the induced drag is minimized when the downwash distribution varies linearly across the span. Note that the moment about the wingroot for a wing corresponds to the heeling moment of a sail rig when coupled with its image system. The planform shapes and lift distributions of Jones' results were more tapered and weighted toward the center of the wing than the elliptical loading. Although the resulting lift distribution produces more drag for a given span than the elliptical lift distribution, the lower moments allowed the span to be increased which reduced the induced drag approximately 14% while keeping the same moment as for the classic elliptical planform.

Lissaman has shown that the a lifting line analysis performed in a nonuniform flow, such as a wind gradient, can be transformed into an equivalent problem in a uniform flow. He also shows that the minimum induced drag is obtained when the induced velocity distribution is a constant. So for the sake of simplicity and clarity, all the results in this paper will be computed for uniform flow.

These criteria suggest a new way to design a sail rig:

1. Establish the constraints on heeling moment (height of center of effort) due

the stability of the hull and any constraints on the height of the rig, such as the need to pass under fixed bridges.

2. Vary the induced velocity distribution so as to minimize the induced drag while

observing the heeling moment constraint, using an inverse method to determine the

spanloading from the induced velocity distribution.

3. Chose section designs based on viscous considerations.

4. Based on the downwash distribution, zero-lift angles of attack of the sections, and

their maximum lift coefficients, establish the combination of twist and planform

shape which results in the most stall margin along the span.

5. Modify the optimum planform to get a shape which can be practically constructed.

6. Analyze the final shape for comparison with the optimal performance.

Since most sections have similar lift curve slopes in their linear range, it is possible to define the twist distributions in terms of the zero-lift angles of attack, and to determine the planform shape independent of the choice of section shape. This enables the designer to examine many design tradeoffs in a very general sense, as will be shown below.

This approach requires both an inverse method and an analysis method. The inverse method is used to compute the optimal spanload and planform shape from the induced velocity distribution. The analysis method is used to analyze the optimal shapes at off-design conditions, and to examine the performance of practical, suboptimal configurations. The lifting line method can satisfy both requirements, whereas lifting surface techniques, such as the vortex lattice method, are almost exclusively analysis methods only.

Lifting Line Method

Lifting line basics. The lifting line method is based on the classical assumptions:

- the lifting surfaces are thin,

- the oncoming flow is steady, uniform, and inviscid,

- trailing vortices are straight and extend to infinity parallel to the apparent wind,

- all velocities are kept small such that small angle approximations suffice for the induced angles of attack.

Figure 2 shows the overall geometry of the lifting line and trailing vortices. Looking upstream, the sail rig appears edge-on, with the lift distribution acting to one side and the induced velocities acting in the opposite direction. The key input parameters which define the geometry of the problem are shown. By appropriate selection of the coordinates for head and foot, any planar configuration can be specified from an upright sail rig to a horizontal wing. For both sails and hydrofoils, the Z axis extends away from the surface - upwards in the case of sails, and down for the case of hydrofoils.

The lifting line is broken up into a number of discrete segments. Each bound vortex segment trails two vortices, one at each end of the segment. The trailing vortices rotate in opposite directions, and all three vortices for a given segment have the same strength.

The Trefftz plane is located at infinity in the downstream direction, so the bound vortices have no effect there. However, the strengths of the bound vortex segments, and their trailing vortices, have to be determined such that there is no flow perpendicular to the segment. The induced velocities in the Trefftz plane are twice those induced at the origin of the wake, since the trailing vortices extend to infinity in both directions from the Trefftz plane, but only in one direction from the sail planform.

The detailed geometry in the Trefftz plane is shown inFigure 3. A control point is located on each segment, and the normal components of the induced velocities from all the trailing vortices
 
 

are summed there. The process is repeated for each segment and the simultaneous equations are solved to determine the vortex strengths.

The induced velocity at point i due to vortex j is given by

1)

where vij is the velocity induced at point i due to a vortex at point j, rij is the radial distance from vortex j to point i, and Gj is the strength of the vortex at point j. wij is the induced velocity component normal to segment i:

2)

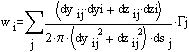
The relationship in equation 2 is applied for each trailing vortex line. Each bound vortex segment actually has four trailing vortices when the corresponding image vortices are included. These images are located at the same distance from the surface, but on the opposite side, and share the same Y coordinate.

The boundary condition for the solid surface is that there be no flow normal to the surface. This requires that the direction of rotation for the image vortices be in the opposite direction for the case of the solid surface. This also approximates the linearized free surface condition in the limit at zero Froude number, when the effects of gravity far outweigh the forces in the flow.

At high speeds, the linear free surface condition is that the pressure on the surface be a constant, which requires that the sum of the tangential velocities induced there must be zero. The surface will have a vertical velocity due to the passage of the hydrofoil. This approximates the behavior of the free surface in the limit at infinite Froude number, when the effects of gravity are negligible when compared to the forces in the flow.

For the case of the solid surface, the matrix elements, mij, are assembled into the overall matrix, M as shown:

k = 1: vortex at beginning of segment (+z, +G)

k = 2: vortex at end of segment j (+z, -G)

k = 3: image vortex of k =2 (-z, +G)

k = 4: image vortex of k = 1 (-z. -G)

3)

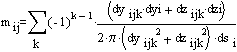
4)

Inverse problem (wi known). At this point, it is easy to determine the optimum span loading (G,) required to minimize the induced drag. According to Munk, to minimize the induced drag for a given span, one need only specify a unit value for all the wi. Since the problem is linear, once the lift coefficient, CL, is found for a unit induced velocity, the induced velocity required to achieve any desired CL can be found by taking the ratio of the lift coefficient for unit velocity to the desired lift coefficient.

5)

6)

Once the lift distribution is known, the twist distribution, ti, is selected, taking into consideration the section zero lift angle of attack, a0, and lift curve slope, ai. With these values, the local angles of attack, ai, can be computed and the planform shape determined.

7)

8)

9)

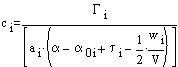
Analysis problem (ci known). The analysis problem begins with the same formulation as the inverse problem. In this case, the chord and twist are known, the downwash velocities are eliminated in order to solve for the lift distribution in terms of the chords:

10)

Validation of Lifting Line Method.
 
 

Results

The inverse lifting line method was applied to determine the characteristics of sail planforms with minimum drag, sail planforms which had reduced heeling moments, and vertical and horizontal hydrofoils operating at high speed. Since the classical semi-elliptical planform is so well known, most of the results are referenced to this planform for comparison.

Some standard definitions:

AR is the aspect ratio, P is the span of the sail rig (e.g. luff length), and S is the total sail area. Di is the induced drag (the net aerodynamic force component due to the lift, acting parallel to the freestream direction), CDi is the induced drag coefficient, r is the fluid density and V is the freestream velocity. L is the lift - the net aerodynamic force component that is at right angles to the freestream - and CL is the lift coefficient.

All of the cases were computed with 20 segments in the lifting line, distributed with cosine spacing. The control points were also distributed using cosine spacing, so they were offset slightly from the center of the segments toward the ends of the span.

Minimum Drag Sail Rigs. For a given span, the minimum drag sail rig has the spanloading which results from a uniform downwash distribution. Figure 4 shows these minimum drag span loadings for gaps between foot and surface that range up to 20% of the span. For zero gap the result is the classical semi-ellipse. Even for very small gaps, however, the optimal loading is quite different. The spanload distribution with gap starts out somewhat egg-shaped, with the point of maximum loading near 40% of the length of the surface. The loading rapidly approaches a full ellipse as the gap is increased.

Assuming that the surface is untwisted, the planform shape will be similar to the spanloading shape. Owing to the constant downwash, the untwisted planform will also have a uniform lift coefficient across its span. Assuming the same section is also used throughout, this will aid in achieving maximum lift, since all parts of the sail will approach the maximum angle of attack together.

The induced drag of the surface is given by

E is the Oswald efficiency factor, and is a function of the planform geometry and the surface effects. The value of e for the minimum drag planforms is shown in Figure 5. For zero gap, e is two, which is in agreement with classic wing theory. With as little as a 1% gap, however, e drops by two-thirds to 1.36. As the span is increased while keeping the gap fixed, E increases slowly. E is actually a function of the gap divided by the span, as can be seen by the fact that surfaces of different size have identical values of e when the gap is sized proportionately.

The lift curve slope for the three-dimensional sail planform is given by

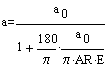
Where a is the lift curve slope (per degree) and a0 is the two-dimensional lift curve slope (per degree). Figure 6 shows the ratio of this formula to the computed results, and the results are shown to agree to well within the numerical accuracy of the method.

The design implications of the minimum drag sail rigs are shown in Figure 7. All data and dimensions are referenced to semi-elliptical planform, which has E = 2 and a height of the center of effort above the surface of 42% of the reference planform's span. This chart can be used to assess the design tradeoffs for a wide variation in planform sizes, simply by changing the reference span, so long as the gap remains less than 20% of the span.

Starting from the reference planform, the induced drag increases rapidly with the introduction of a gap. Eventually, the curve at the right hand edge of the carpet plot would become asymptotically vertical at a value of two, as the gap becomes very large and e drops to its classic value of one for an isolated planar planform. If the gap is kept fixed and the head of the sail rig is raised, the induced drag drops and the center of effort goes up. Eventually, these curves would become vertically asymptotic to the Y axis as the flow becomes increasingly two-dimensional.

Reduced Moment Sail Rigs. The heeling moment of the sail rig can be reduced by changing the design induced velocity distribution so that it tapers linearly from a maximum value at the foot to a minimum value (which may be negative) at the head. In principle, there is no limit to one's placement of the center of effort, provided that it is permissible to have negative lift at the head of the sail. It is even possible to have the center of effort at the surface for complete cancellation of the heeling moment. However, there are practical limits to this, as will be seen.

Reduced moment, minimum induced drag spanloadings corresponding to the previous cases were computed using triangular downwash distributions which had a maximum value at the foot, and went to zero at the head. The resulting spanload distributions are shown in Figure 8. Compared with the minimum drag lift distributions, these are more tapered toward the head and weighted toward the foot. The point of maximum loading is at approximately 30% of the span compared to 40% to 50% for the minimum drag loadings.

There is not a unique planform which corresponds to these loadings. If an untwisted planform is adopted, it will have a similar spanloading at all angles of attack. However, it will be very sharply tapered toward the head, and the head will operate at a much higher angle of attack (owing to the tapered induced velocity distribution) than the foot of the sail, making it prone to stall. A better solution is to apply a twist that is parallel to the induced velocity distribution, washing out the head so as to maintain a constant angle of attack across the span. The required twist distribution is shown in Figure 9. The twist (in degrees) for this particular choice of induced velocity distribution can be seen to approximate the following relation:

Where t0i is the twist applied to the zero-lift angle of attack - the aerodynamic twist. For a design lift coefficient of one and an aspect ratio of four, the resulting aerodynamic twist is around seven degrees. This can be achieved with either physical twist of the planform or a change in camber, or both. If the camber is increased towards the head, as is common practice, the physical twist will be greater than seven degrees. With this twist distribution, the sectional lift coefficient is once again constant and equal to the surface lift coefficient, and the planform shape is similar to the spanloading shape. These shapes bear a remarkable resemblance to boardsail planforms, so it can be seen that the rapid, unfettered evolution in board sails has settled onto something very similar to these optimal shapes.

Because of the twist, the spanloading can be broken down into a basic lift distribution and an additional lift distribution. The basic lift distribution is the spanloading that would be obtained if the sail were operated at the angle of attack for zero lift and the twist was held fixed at the design values - like a tin sail in the wind tunnel. This basic lift distribution is shown in Figure 10. Although the net lift is zero, the local lift varies up to over 20% of the design lift coefficient; negative near the head, and positive near the foot. This is an aerodynamic couple in the anti-heeling direction, and it is this couple which supplies the reduction in the center of effort for these planforms.

The additional lift distribution is the change in the spanloading for a change in angle of attack or surface lift coefficient. It can be found by subtracting the basic lift distribution from the design spanloading and dividing by the angle of attack or design lift coefficient. Owing to the taper in the planform, the additional lift distribution is proportionately greater at the head than at the foot. This is shown in Figure 11, which shows the change in sectional lift coefficients that result from a unit change in the surface lift coefficient. These range from less than 80% of the change in surface lift coefficient at the foot to over 150% at the head.

The span efficiencies for these reduced moment design spanloadings are shown in Figure 12. These are approximately 10% or more lower than the corresponding minimum drag spanloadings because of the switch from uniform induced velocities to tapered induced velocities.

As seen in Figure 13, the same expression for the three-dimensional lift curve slope holds, provided that the new values of E are used. Since the aerodynamics are linear, the magnitude of the lift distribution is proportional to the magnitude of the induced velocities, as is the twist distribution. So the value of the lift curve slope holds for other angles of attack provided that magnitude of the twist distribution is also varied with the angle of attack.

The design tradeoffs for the reduced moment sail planforms (triangular induced velocity distribution) is shown in Figure 14. Once again, the data are relative to the semi-elliptical planform, which is also indicated on the chart for reference.

The height of the center of effort isn't the whole story with regard to heeling moment for a twisted planform, however. Such a planform has an aerodynamic center which is different from the center of effort. The aerodynamic center is defined as the location about which the moment is a constant as the angle of attack is changed. The center of effort (or the center of pressure), which is the location at which the moment is zero, will move up and down as the lift changes.

Although the yacht may have adequate stability when the moments are balanced with the design lift acting at the design center of effort, the effect of gusts will be different. The increased loading of the additional lift distribution means that the incremental effects of gusts will be applied at the aerodynamic center, not the center or effort. The dashed lines in Figure 15 show the position of the aerodynamic center for the reduced moment planforms, compared to the centers of effort from Figure 14 (solid lines). The aerodynamic center is always higher than the center of effort for these planforms, because of the anti-heeling moment of the basic lift distribution. For the case of untwisted planforms, like the previous minimum drag planforms, the location of the center of effort and the aerodynamic center are the same.

In effect, the basic lift distribution is acting like water ballast which has been moved to windward to balance the boat, and the lift is effectively acting at the aerodynamic center. So it is important to consider the height of the aerodynamic center when doing stability calculations as well as the height of the center of effort.

Now consider taking the reduction in heeling moment to its practical extreme. Figure 16 shows the resulting lift distributions when the induced velocity distribution is adjusted so that the lift chord distribution goes to zero at the head. This requires an induced velocity distribution which is positive at the foot and negative at the head, varying linearly in between. As with the previous reduced moment planforms, the twist distribution (Figure 17) is set so as to maintain a constant section lift coefficient across the span, but the twist is more than doubled. Any more twist (more negative induced velocities at the head), and the sail will produce negative lift at the head, which is either not physically realizable or would require a separate surface with its own deflection.

Again, since the lift coefficient is constant, the planform shape is similar to the spanload distributions shown in Figure 16. These planforms resemble the conventional triangular sail, except that the maximum chord is not at the foot, but occurs 20% to 25% of the length above the foot.

All of the planforms presented bear some resemblance to conventional sail rigs, except for the position of maximum chord. It would appear that cutting away the area at the clew and redistributing it elsewhere would improve the performance of most sail rigs. The large chord at the foot results in a rapid change in the lift at the foot, which sheds a stronger trailing vortex there than is necessary, increasing the induced drag and making the largest area of the sail comparatively ineffective.

The basic lift distribution shown in Figure 18 is also twice that of the previous case, and the additional lift distribution shown in Figure 19 indicates that the pointed tip will be way over-loaded for any significant increase in angle of attack over the design values.

Finally, Figure 20 puts together the whole sail rig center of effort vs. induced drag tradeoff. The solid lines indicate the minimum drag planforms. The dashed lines show the centers of effort for the triangular induced velocity distribution planforms, and the dash-dot line shows the practical limit for reducing the center of effort of the rig.

The reduced moment designs all have a lower center of effort and greater drag than their uniform induced velocity counterparts. However, by following up the lines of equal gap, one can see that by lengthening the span of the reduced moment design, one can reduce the drag over the minimum drag/fixed span design while not accepting any additional heeling moment.

But what about the center of effort? Figure 21 shows that there is no free lunch here. The drag tradeoff in center of effort for the reduced moment designs is the same as for the minimum drag designs. However, the picture with regard to gust response is better than this chart would indicate.

By definition, the basic and additional lift distributions assume that the twist is not a function of angle of attack. However, if the twist is varied with the angle of attack, as shown in equation X, then the center of effort and the aerodynamic center will coincide once again, and the drag reductions shown in Figure 20 can be realized even when the gust response is considered. This is basically what is happening with modern fat-headed sails in which the head of the sail is allowed to twist off under increased loading.

Figures 20 and 21 indicate what is possible in planform design. Other planforms will have greater induced drag for the same center of effort because of their non-optimal induced velocity distributions. However, practical planforms can be constructed which come close to these, so these charts are useful for showing the designer what performance is possible.

Vertical Hydrofoils. The same criteria for minimizing the induced drag of sail rigs applies to hydrofoils and hulls. In this case, the moments are not as important because the hydrofoils (such as keels and rudders) are not as long as the sail rigs, and because the span is typically more constrained. Therefore, only the results for minimum drag with a fixed span will be presented.

The present method cannot handle the nonlinear effects of waves in a free surface. However, it can handle the two limiting cases of very low speed and very high speed, in which the surface can be considered flat and the perturbation of the surface shape is small. For the low speed case, the water surface acts like a solid boundary and all the results previously presented for sail rigs apply.

For high speeds, corresponding to chord Froude numbers (V/(g*c)0.5) about roughly two and planforms of moderate to high aspect ratio, the infinite Froude number approximation gives reasonable results (Kuhn and Scragg, 1993). For this approximation, the image system used to enforce the surface boundary condition is the same for the solid surface, but the signs of the vortex strengths are reversed.

The linearized free surface boundary condition was applied to determining the minimum drag spanloads for vertical hydrofoils, as shown in Figure 22. Once again, the planform shape is similar to the load distribution due to the uniform induced velocity distribution and the lack of twist. Compared with the corresponding solid surface shapes, the area nearest the surface is reduced and the profiles have an inverted egg-shape.

With zero gap, the span efficiency factor E, shown in Figure 23, is 0.81 - a 19% reduction from the isolated planar wing case, and only 40% of the value for the semi-elliptical solid boundary case. The efficiency grows and the shapes become more elliptical as the hydrofoil is designed for conditions farther from the surface.

Figure 24 shows the center of effort/induced drag design tradeoffs for the minimum drag vertical hydrofoils. As before, all data are referenced to the geometry and results for the semi-elliptical planform at a solid boundary. Also shown are the results for the solid boundary case and for the elliptical planform in an infinite fluid.

For the surface piercing foil, the design location of the center of effort is not greatly different from that of the infinite fluid case, but the best one can do is to limit the increase in induced drag to approximately one quarter of the latter.

Horizontal Hydrofoils. Flying hydrofoils are also concerned with minimizing the drag of horizontal hydrofoils. There are two types of surface effects to consider - chordwise surface effects and spanwise surface effects. The former is concerned with the change in the section pressures as the hydrofoil approaches the free surface. This tends to reduce the sectional lift curve slope. The spanwise surface effects have to do with the change in induced drag and the three-dimensional lift curve slope due to the change in effective span as the hydrofoil approaches the surface, and these are the surface effects considered here.

Figure 25 shows the minimum drag spanloads for the horizontal hydrofoils computed with the linear free surface approximation and uniform induced velocity distribution. The shapes for all depths are elliptical. Since the design shapes are the same, these results apply for both foils designed for different depths, and for elliptical foils which are moved up and down.

The best span efficiency (Figure 26) for hydrofoils operating at the surface is 0.5, which corresponds to the planing condition. E increases as the depth is increased, and is over 0.9 when the hydrofoil is one semi-span below the surface.

Wings in Ground Effect. For the sake of completeness, Figure 27 and Figure 28 present the spanload/chord distribution for wings designed to operate near a solid boundary. These are also minimum drag planforms, having a uniform induced velocity distribution. As the wing is designed to operate successively closer to the surface, the planform becomes more tapered and the efficiency goes up very rapidly. This occurs because the image system is canceling the trailing vortices shed by the wing.

Summary. The span efficiency factor, E, is shown in Figure 29 for all the planar lifting surface cases considered. All the points in this figure represent design conditions, and do not represent the effects of moving a given planform closer or farther from the surface. The horizontal hydrofoils are the only exception to this.

Once E is determined, the three-dimensional lift curve slope can be calculated from equation Y. The induced drag can be computed from equation YY. Provided the optimal twist is used (if any), the section lift coefficients will be the same as the planform lift coefficient.

Knowing the section lift coefficient and the spanload distribution, the chord distribution can be determined based on the local section lift-curve slope. Note that this makes it possible to take into account such effects as the loss of lift due to separation at the leading edge caused by the mast, by simply making the chord larger where the section lift curve slope is less. Finally, the geometric twist can be determined, based on the optimal aerodynamic twist and the zero lift angles of attack of the sections.

References

1. Day, A. H., "Sail Optimization For High Speed Craft", Transactions of Royal Institution of Naval Architects Vol. 133, 1991.

2. Day, Sandy, "The Design Of Yacht Sailplans For Maximal Upwind Speed", Twelfth Chesapeake Sailing Yacht Symposium, January 1995.

3. Greely, D.S., Kirkman, K.L, Drew, A. L., Cross-Whiter, J., "Scientific Sail Shape Design", Ninth Chesapeake Sailing Yacht Symposium, March 1989.

4. Jones, Robert T., "The Spanwise Distribution Of Lift For Minimum Induced Drag Of Wings Having A Given Lift And A Given Bending Moment", NACA-TN-2249, 1950.

5. Lissaman, Peter B. S., "A Numerical Solution For The Minimum Induced Drag Of Nonplanar Wings", AIAA Journal of Aircraft Vol. 5, No. 1, pp 17-21, Jan-Feb 1968.

6. Lissaman, Peter B. S., "Lift In A Sheared Flow", AIAA Ancient Interface Symposium (year unknown, probably late '70's).

7. Kuhn, John C. and Scragg, Carl A., "Analysis of Lift and Drag on a Surface Piercing Foil", Eleventh Chesapeake Sailing Yacht Symposium, January 1993.

8. Munk, Max M., "The Minimum Induced Drag Of Aerofoils", NACA Report No. 121, 1923.

9. Schlichting, Hermann and Truckenbrodt, Aerodynamics of the Airplane, McGraw-Hill International Book Company, 1979.

10. Wood, C. J. and Tan, S. H., "Towards An Optimum Yacht Sail", Journal of Fluid Mechanics, Vol. 85 Part 3 pp. 459-477, 1978.