This is the derivation of a simple velocity prediction program (VPP) for landyachts.  A working Mathcad version of this program can be found here.  Although it was derived for landyachts with rigid wing rigs, the program can be adapted to any sailing vehicle by replacing the rolling resistance equations with the appropriate hull drag and sideforce model.  By replacing a few key geometry and aerodynamic parameters, it is easy to see the effects of major design choices on the performance of the yacht.

The following assumptions are made:

1. pilot trims sail to the angle of attack for either best L/D or maximum lift under light to medium winds, but will reduce alpha to keep wheel on ground or to avoid skidding in high winds

2. variation of yacht parasite drag with apparent wind angle is neglected

3. aerodynamic drag coefficient follows a parabolic polar based on wing lift coefficient

4. rolling resistance is linearly dependent on vertical and side loads

5. rolling resistance varies linearly with speed (consistent with the existing limited test data)

Basic kinematic relationships:

Fundamental speed relationship:

Force relationships:

gamma : direction of travel relative to true wind
beta : angle between apparent wind and direction of travel
Vb_Vt : ratio between yacht speed and true wind speed (Vb/Vt)
Va_Vt : ratio between apparent and true wind speeds (Va/Vt)
Ds : aerodynamic drag on whole yacht
Ls : aerodynamic lift on whole yacht
L_D : ratio of aerodynamic lift to drag (L/D)
Dw : total rolling resistance
Lw : total sideforce from wheels
rho : air density
S : wing area
CDo : Parasite drag coefficient of whole yacht
Ki : induced drag coefficient
Kwv: viscous rolling resistance coefficient due to vertical load
Kws: viscous rolling resistance coeffcient due to side load
Kwf: static rolling resistance coefficient (after breakout)
mu : lateral friction coefficient
W : yacht gross weight
Dwref_W : ratio of viscous rolling resistance to weight at a reference speed

Balance of forces:

Moment Balance

(vertical center of drag is not same as vertical center of lift because of parasite drag of body.  So ignore parasite drag of wing (it may be small compared with body) and only look at lift induced forces)

Di : induced drag
epsilon-w : angle between centerline & wheel centers
Hce : height of center of effort
Ycg : distance from CG to line connecting wheel centers

Sail trim for best L/D:

Sail trim if constrained by rolling moment:

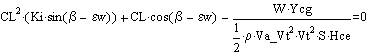
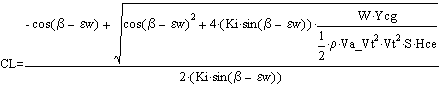
Sail trim if constrained by skidding:

by substitution, yields

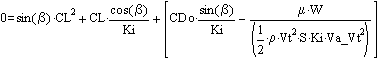
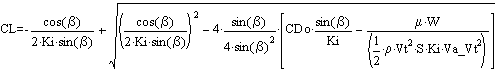
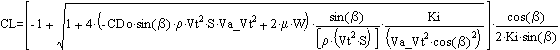
Approximate axle sizing (so skidding & heeling happen at about the same time)

Rolling resistance defined in terms of drag of yacht sailing at some reference wind velocity (say, 10 mph). This is to be consistent with the generic performance analysis and a convenient way of incorporating existing tow data.

Substituting into the Dw force balance equation gives the performance relationship:

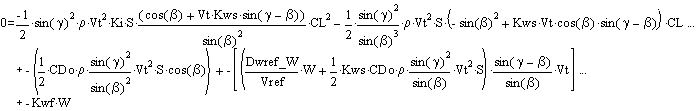
COMPLETE PERFORMANCE ANALYSIS

Numerical tolerance for iterative solutions:

Yacht Parameters:
Area (Class V) :

Aspect Ratio :

Oswald efficiency :

Height of CE :

CDo :

CLmax :

Gross Weight :

Friction Coefficient :

Rolling Resistance :

Sideforce Resistance:

Reference Speed :

Wheel Apex Angle :

Axle Size:

Length of yacht from front wheel to c.g.:

Sail Trim:

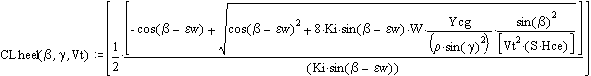
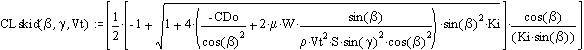
(reset CL to CL max -- the second trim strategy)

Yacht Acceleration:

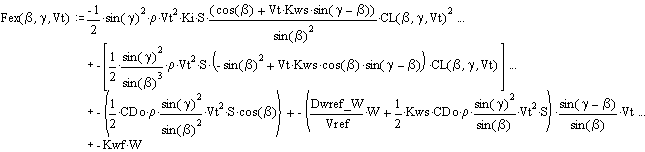
10mph:

15mph:

20mph:

25mph:

30mph:

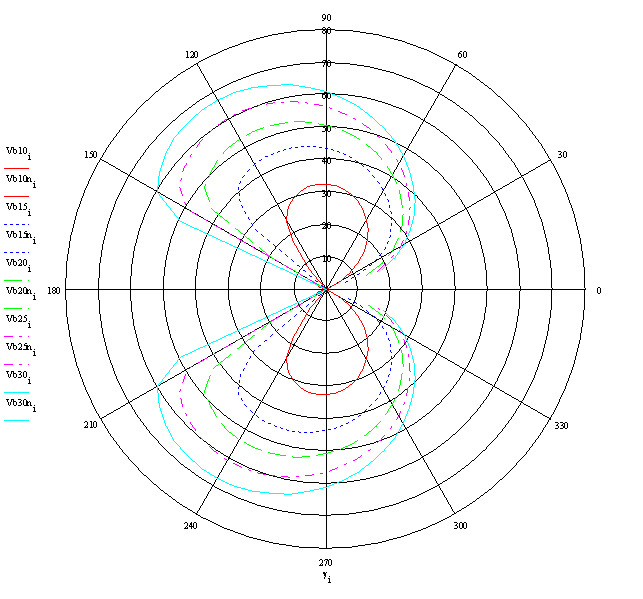
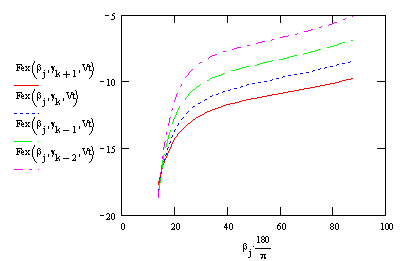
Plot excess thrust vs beta to see if there will be any problems with convergence in the iterative solution:

Final Results (wind is from 0 degrees):

Home